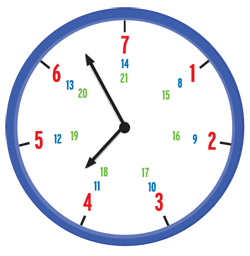
This type of unconventional clock is commonly used to illustrate problems in modular arithmetic. This particular clock has 7 “hours”; each “hour” position holds a set of numbers that are congruent modulo 7, or separated by multiples of 7. For one particularly elusive set of equations, earlier mathematicians located an ingenious but labor-intensive solution method in modular arithmetic. Richard Taylor’s work finds a shortcut in geometry.
As academics work to understand the architecture of the universe, they sometimes uncover connections in mysterious places. So it is with Smith professor of mathematics Richard L. Taylor, whose work connects two discrete domains of mathematics: curved spaces, from geometry, and modular arithmetic, which has to do with counting. Taylor has spent his career studying this nexus, and recently proved it is possible to use one domain to solve complex problems in the other. “It just astounded me,” he says, “that there should be a connection between these two things, when nobody could see any real reason why there should be.”
This is not the first instance of finding in geometry an elegant explanation for a seem- ingly unrelated phenomenon. Scholars during the Renaissance, seeking a mathematical basis for our conceptions of beauty, fingered the so-called Golden Ratio (approximately 1.6 to 1). Some analyses find the ratio in structures—most famously the Parthenon—built centuries before its first written formulation. More recently, scientists have found that the faces people find most beautiful are those in which the proportions conform most closely to the ratio.
The geometry-arithmetic connection explored by Taylor solves another puzzle that has enticed mathematicians across centuries. In 1637, French mathematician Pierre de Fermat scrawled in a book’s margin a theorem involving equations like the one in the Pythagorean theorem (a2 + b2 = c2), but with powers higher than two. Fermat’s theorem said such equations have no solutions that are whole numbers, either positive or negative. Go ahead, try—it is impossible to find three integers, other than zero, that work in the equation a3 + b3 = c3.
The French mathematician also wrote that he had discovered a way to prove this—but he never wrote the proof down, or if he did, it was lost. For more than 350 years, mathematicians tried in vain to prove what became known as Fermat’s Last Theorem. They could find lots of examples that fit the pattern, and no counterexamples, but could not erase all doubt until Princeton University mathematician Andrew Wiles presented a proof in 1993.
His discovery made the front page of the New York Times, but six months later, the Times reported that another mathematician had found a mistake in the new proof. In the spotlight and under pressure, Wiles called on Taylor, his former doctoral student, for help. Together, they published the corrected proof in 1995, and Wiles won the Fermat Prize for mathematics that year. Taylor won the same prize in 2001, and last year shared the prestigious, million-dollar Shaw Prize for proving the 1963 Sato-Tate Conjecture, which said that one could draw a curve that would predict the number of solutions for any equation describing an elliptic curve.
The conjecture itself was a brilliant insight, but applying it is labor-intensive—it relies on modular arithmetic, a domain of mathematics that studies the relationships between numbers, often illustrated using clock-like figures with unusual numbers of hours (i.e., not 12). Counting the number of solutions for an equation required counting one’s way around the “clock” (see figure at right). In proving the conjecture, Taylor essentially mapped the directions for a massive shortcut. But the proof was, as Taylor puts it, “a nice by-product” of his main work on the connection between arithmetic and geometry.
Taylor’s Shaw Prize co-recipient, mathematician Robert Langlands, had been the first to realize, back in the 1970s, that instead of counting the number of solutions for these equations, it would be possible to get the same answer using geometry. Specifically, the shortcut lay in the symmetry of hyperbolic space, one of the mathematical concepts illustrated by the artist M.C. Escher. In this weird, warped world, pairs of parallel lines break all the laws of Euclidean geometry and bend away from one another, and lines that, to the human eye, look wildly different are actually the same length. The analogy commonly made is to a horse’s saddle: viewed from above, a saddle appears as an oval, but its circumference is unexpectedly long because it curves downward along the sides of the horse’s body and upward toward the horse’s head and tail.
Although Taylor teaches everything from undergraduate calculus to advanced graduate courses, his primary research is work on a kind of foreign-language dictionary that translates between these two mathematical domains—between the language of clocks and that of saddles. Taylor describes the dictionary this way: “It says, ‘Here’s an equation. I’m going to give you a problem about symmetry that has the same behavior.’” He and other number theorists are busily filling in more entries to illustrate patterns and perhaps solve still-unidentified mathematical mysteries. “We’ve done A and B so far,” he says. “All the way up to Z is left.”
~Elizabeth Gudrais








